弯管塑性发展过程与失效模式分析

 选取参数k=5,R./R;=2,c/a=0.6,c/t=0.4 的情况研究含半椭圆裂纹厚壁弯管的塑性变形过程。有限元模型及边界条件情况与极限荷载求解时完全一致，荷载步施加采用的是荷载步文件加载法，共设置6个荷载步，每个荷载步求解10个子步，第1荷载步施加200 MPa内压，第2荷载步施加300 MPa内压，依次类推，第6荷载步施加塑性极限荷载677.8MPa内压。

 由图5-8为t=1.1s 时对应的 Mises 应力分布图，该子步对应的内压力P;=210 MPa.由图中可以看出，在弯管内侧裂纹自由面处，最大应力为875 MPa,超过材料的屈服极限，弯管开始出现塑性屈服。弯管内表面其他区域应力分布较均匀，大小在450MPa左右。图5-9为t=2.1s时的Mises 应力图，该子步对应的内压力P=310 MPa.由图中可以看出，随着内压力的增加，裂纹自由面处始终是应力最大点，最大应力为 891 MPa.裂纹自由面附近的塑性区范围开始扩大，并沿着管轴方向扩展，内表面应力分布开始不均匀，内侧内壁应力明显大于其他区域。

 图5-10为t=3.2s时对应的Mises应力分布图，该子步对应的内压力P;=420 MPa.由图中可以看出，在该时刻下，弯管内侧内壁应力超过800 MPa,首先达到屈服。最大应力不再出现在裂纹自由面处，而是在内壁屈服扩展方向的末端。图5-11为t=3.6s时对应的Mises应力分布图，该子步对应的内压力P1=458 MPa.由图中可以看出，在该时刻下，弯管外侧内壁应力值为850MPa左右，紧接着达到屈服。最大应力出现在外侧内壁屈服扩展方向的末端。

 图5-12为t=5.9s时对应的Mises应力图，该子步对应的内压力P;=670 MPa.由图中可以看出，在该时刻下，弯管内表面已经完全屈服，且塑性区已经沿着壁厚方向扩展，几乎接近弯管外表面。图5-13为t=6s时对应的Mises应力图，该子步对应的内压力为极限荷载678.7 MPa.由图中可以看出，在极限荷载作用下，塑性区已经穿透壁厚，弯管内侧外壁出现较大塑性区，外侧外壁并没有塑性区的出现，但弯管实际已经失去继续承载能力。

  由上塑性发展过程可以总结出，在一定内压作用下，首先在裂纹自由面处产生局部屈服，最大应力同时出现在该处，但不会出现塑性铰。随着内压荷载继续增大，应力应变发生重分布，裂纹自由面不再是最大应力出现的位置，同时塑性区沿着内表面轴向发展较快，沿着壁厚方向扩展较慢。当内压达到极限状态时，弯管内表面完全屈服，塑性区穿透内侧壁厚，弯管失效，失效模式为整体破坏。

进入后处理器，在已经发生屈服的弯管内表面上选取一个节点，以总应亦光 阿亦具光V她作中时间－应亦关系网，如图5-14所示。

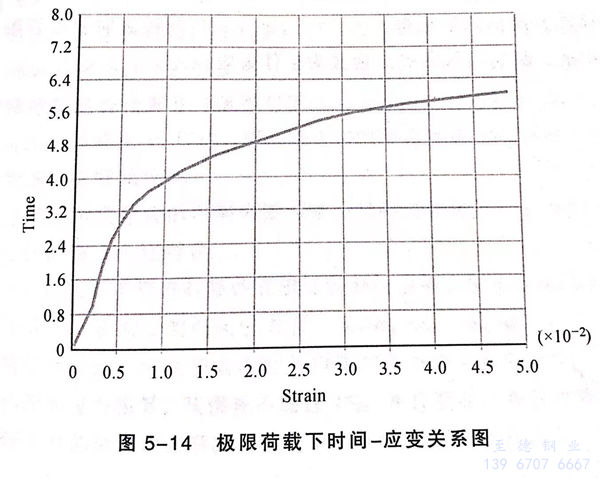
可以看出，在加载初始段，节点的总应变随着荷载增加而线性增大。在弹性极限荷载处（t=3.2s)曲线斜率发生明显转折，荷载增加缓慢而应变增加迅速。到达极限荷载时，曲线斜率接近水平，即在较小的荷载增量下，应变保持持续增长，这间接验证了本书计算结果的正确性。