含半椭圆裂纹弯管极限荷载的数值分析

1. 单元选取及边界条件设置

 SOLID185 和 SOLID186 单元的结构和节点布局分别与 SOLID45和SOLID95 单元基本相同，但前两者的组合更能准确模拟裂纹尖端的非线性行为，且具有塑性、大变形及大应变、应力强化等特性，是模拟含裂纹结构弹塑性行为的最佳单元。单元几何构型同图4-9和图4-10。

 为了节省计算机时，选取 1/4 模型进行计算，除了直管段外缘节点施加位移全约束外，弯管1/2剖面和45度截面上分别施加相对X-Z和X-Y平面的正对称约束。

2. 最经济单元数试算确定

 为了减少非线性求解最大迭代次数又不降低计算结果的精度，本节中通过试算几组不同的非裂纹体轴向单元划分和环向单元划分，最后确定最经济的单元划分为：轴向划分15份，环向划分5份，最终得到的1/4模型的单元总数为993,节点总数为1073,以下结果均是在这一试算结果下得到的。

3. 极限荷载计算结果

选择的材料及其力学性能参数同光滑弯管相同，设置初始参数t=0.2m,将不同参数配置下含半椭圆裂纹厚壁弯管极限荷载 PL的结果列在表 5-1中，单位MPa.

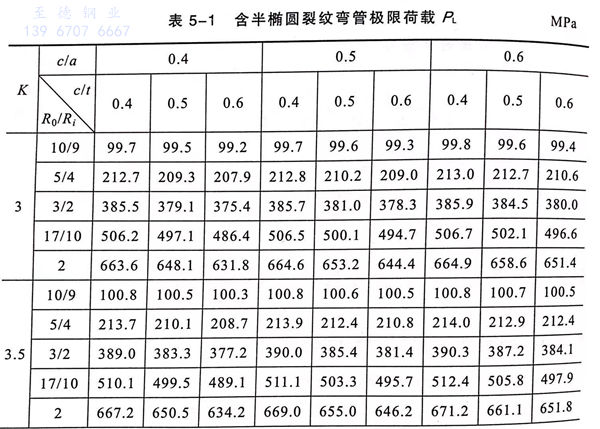
4. 极限荷载随影响因素变化规律

影响含半椭圆裂纹弯管极限荷载的因素主要有：弯管结构参数－径比（R./Ri)、几何参数－弯曲半径比（k)、裂纹几何参数－形状比（c/a)和深度比（c/t).

 根据表5-1中的数据，分别作出PL值随影响因素的变化关系图，并给出分析说明：

（1)图5-2给的是R./R;=3/2、c/a=0.5时，PL值随k变化的关系图

由图可以看出，极限荷载PL值随k的增加而增大，说明含裂弯管弯曲程度越低，其极限荷载越大，这与光滑弯管的情况一致。

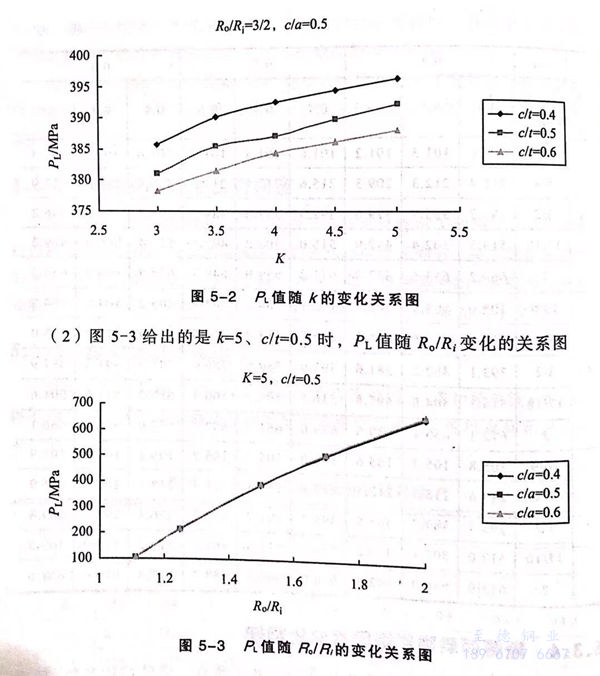
由图可以看出，极限荷载PL值随R./R;的增加而增大，说明含裂纹弯管壁越厚，其极限荷载越大，这也与光滑弯管的情况一致。

（3)图5-4给出的是k=5、R./R;=3/2时，PL值随cla变化的关系图

由图可以看出，极限荷载PL值随c/a的增加而增大，说明椭圆裂纹形状越圆，其极限荷载越大，形状越扁，极限荷载越小。c/t=0.4与c/t=0.6的曲线相比，变化趋势相对缓和，说明椭圆裂纹较深时，PL值随c/a的变化幅度会比较大。

 由图可以看出，极限荷载PL值随c/t的增加而减小，说明椭圆裂纹越深，其极限荷载越小，裂纹越浅，极限荷载越大。c/a=0.4与c/a=0.6的曲线相比，变化趋势相对剧烈，说明椭圆裂纹形状越扁时，PL值随c/t的变化幅度会更大。

为了研究含半椭圆裂纹厚壁弯管相对于光滑弯管极限荷载的降低程度，需要定义一个无因次参量 M(PL/PLO)为削弱系数，PL表示含裂纹时的极限荷载，PL.表示光滑时的极限荷载。M值列在表5-2中。

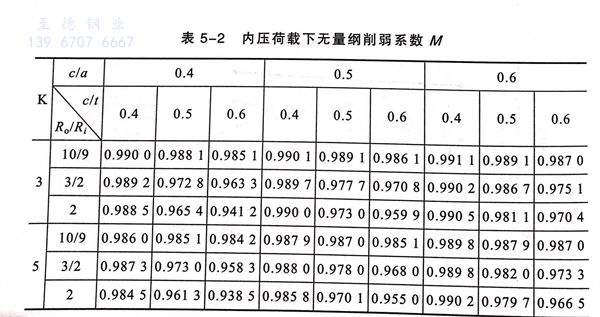
（5)图5-6给出的是k=5、R./R,=3/2时，M值随cla变化的关系图

由图可以看出，削弱系数M随cla的增加而增加，说明椭圆裂纹形状越圆，裂纹的存在对弯管极限荷载的削弱程度越小，反之，对极限荷载的削弱程度越大。c/t=0.4与c/t=0.6的曲线相比，变化趋势相对缓和，说明椭圆裂纹较浅时，裂纹对弯管极限荷载的削弱影响不明显，而裂纹较深时，削弱程度较大。

（6)图5-7给出的是k=3、R./R;=3/2时，M值随c/t变化的关系图

由图可以看出，削弱数M随c/t的增加而减小，说明椭圆裂纹越深，裂纹的存在对弯管极限荷载的削弱程度越大，反之，对极限荷载的削弱程度越小。cla=0.4与c/a=0.6的曲线相比，变化趋势相对剧烈，说明椭圆裂纹形状越扁时，裂纹对弯管极限荷载的削弱程度越大，而形状较圆时，削弱程度较小。

5. 带不同长度直管段弯管的极限荷载

 实际弯管的使用当中，弯管端部总是和其他结构件（如直管、法兰等）相连接，本节针对上文采用的直管段固定约束的有限元模型，考察带有不同长度直管段的含裂纹弯管的极限荷载变化情况。

 选取无量纲直管段长度L/D作为分析参数，D为弯管外直径。L/D=0.5、3、5、10、20时，内压作用下计算得到的无量纲极限荷载M值如表5-3所示。由表中数据可以看出，L/D从0.5增加到20,M呈下降趋势且下降幅度最大不超过1%,完全可以忽略直管长度对极限荷载求解的影响。