含半椭圆裂纹不锈钢厚壁弯管在弯矩作用下的弹性有限元分析

1.  ANSYS中弯矩荷载的施加方法

 作用于不锈钢弯管平面内的弯矩，其方向可以分为使弯管张开或闭合两类。根据文献的理论分析，弯管承受张开弯矩的能力要高于承受闭合弯矩的能力，从保守角度出发，本书考虑闭合弯矩荷载作用的情况。

  ANSYS中弯矩的加载方法一般有三种：一是将弯矩转换成一对一对的力偶，直接施加在对应的节点上面。二是在构件需要加弯矩的节点附近建立一个关键点，然后用MASS21单元进行划分，得到主节点。接着选择需要施加弯矩的节点作为从节点，用CERIG命令建立约束方程，形成刚性区域。最后直接加弯矩到主节点上即可。三是使用MPC184单元。在需要加弯矩的节点附近建立一个主节点，选择单元类型为MPC184单元，用节点生成单元的命令逐一将主节点与其他从节点生成多根刚性梁单元，从而形成刚性面。最后也是直接加荷载到主节点上，通过刚性梁来传递弯矩荷载。笔者经过试算发现，用上面三种方法计算得到的结果基本一致。但是需要注意的是，CERIG 命令使用的前提是小变形理论，即仅在发生小位移或是小旋转时才能用，而第三种方法适用多种场合，不仅支持大应变，还支持非线性情况。本书选用的是方法二，并按照第4.3.3节的加荷方法施加弯矩荷载。

2. 含半椭圆表面裂纹不锈钢厚壁弯管的应力分布

 本节中，分别给出表4-1初始参数下光滑弯管和含半椭圆裂纹弯管在弯矩荷载作用下的 Mises 应力分布图，并结合内压作用下的应力分布情况进行比较说明。

 由图 4-22 可以看出，最大Mises 应力发生在弯管内侧外壁，其值为8.4 MPa,最小值发生在弯管远端（直管段）的中心线上，其值为0.2 MPa,从内侧外壁和外侧外壁向中心线处，Mises 应力值均匀的由大变小。与弯管受内压作用下的情况比较，在弯矩荷载作用下，按材料发生屈服的易难程度排序的结果是：内侧外壁＞外侧外壁＞内侧内壁＞外侧内壁。这与内压下的屈服规律完全不同，即在弯矩荷载作用下，内侧外壁面才是最危险面，换言之，出现在这个位置的裂纹才是最危险的。图4-23为含半椭圆裂纹时的 Mises应力分布情况，与光滑弯管相比，由于应力发生了重分布，应力梯度变化更小，分布更趋于均匀，弯管中心线处依然是应力最小的位置但面积更大。

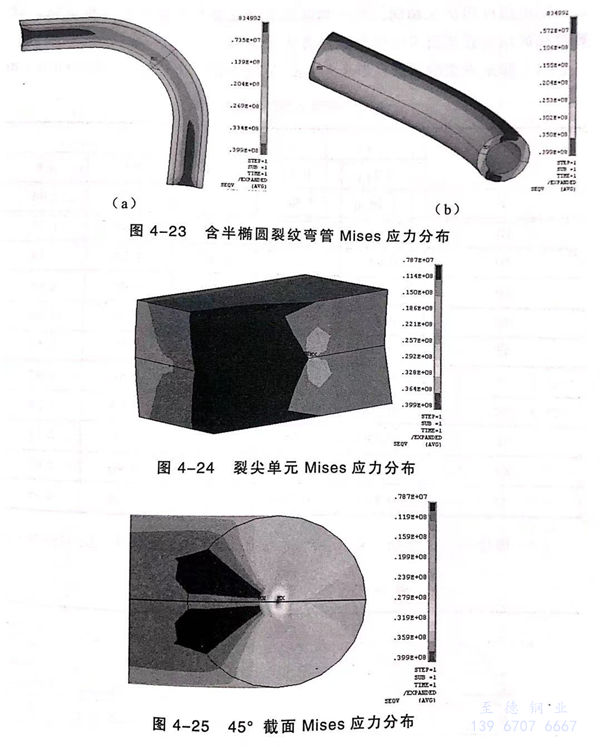
 图4-24为裂尖单元和过渡单元的Mises应力分布情况、与内压循况相同，最大Mises应力23MPa出现在弯管内壁裂纹的自由表面处，第二大应力出现在裂纹最深点、其值为21MPa、位于内压下做的水平制切图做比较、图-25是在裂纹前绿45度位置处做的垂直切片应力图、外圆线框是裂纹课。由图可以清断地看到队内侧内壁到内侧外壁的应力过度情况。

 综上来看，可以得出以下结论：弯矩作用下弯管最易屈服的位置在内侧外壁，这一位置的裂纹是最危险的；由于裂纹的存在，应力会发生重分布，但是相比内压下的分布还不是很均匀。

3. 应力强度因子K的术解

同内压作用情况相同，在已建好的有限元模型上施加纯弯矩荷载，计算得到的应力强度因子结果列人如表4-9~表4-13中。

（1) 假定不变的参数：K=3、R./R.=3/2

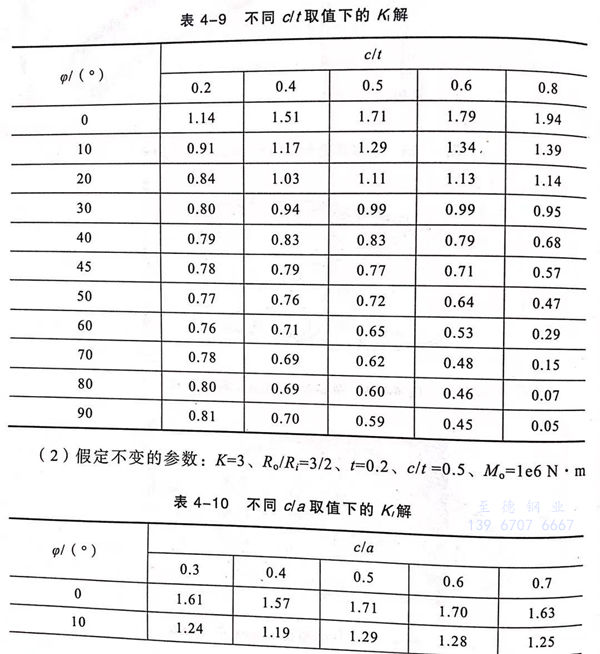
4. 应力强度因子的影响因素及变化规律

针对以上5组表格的K1值，分析其在弯矩荷载作用下随影响因素的变化情况。

（1) 图4-26给出的是不同c/t取值下K1值随φ的变化关系图

从数值变化情况来看，在弯矩荷载1000kN·m作用下，K1值最小为0.05,发生在c/t=0.8曲线的90°位置处；K1值最大为1.94,同样发生在c/t=0.8曲线上，但位置在裂纹的自由表面处。整体K1数值变化幅度不大，且从裂纹自由表面（0°)到裂纹最深点（90°),K1值呈下降趋势。从曲线形态来，弯矩作用下K1值随c/t的变化规律与内压下的完全不同，五条曲线在大约40°位置处相交，以40°为界，clt对K1值的影响能力发生转折。0°~40°一段，裂纹较深（c/t=0.8)时相对裂纹较浅（c/t=0.2)时有更大的K1值，这说明在这一角度范围内，裂纹较深时对K1值的影响能力更大；40°~90°一段的情况正好相反，裂纹较浅时相对裂纹较深时有更大的K1值。c/t=0.8对应的曲线变化较剧烈，而c/t=0.2对应的曲线变化较平缓。

（2) 图4-27给出的是不同cla取值下K1值随φ的变化关系图

 从数值变化情况来看，在弯矩荷载1000kN·m作用下，K1值最小为0.43,最大为1.71,整体K1数值变化幅度不大。从曲线形态来看，五条曲线基本保持平行关系且随角度的增大而下降，即对每一种cla都有在裂纹自由表面的K1大于纹深处的K1.沿纵坐标观察发现，cla越大（椭圆越圆），K,值越小，对应的奇异应力场越弱；反之，cla越小（椭圆越扁），K1值越大，对应的奇异应力场越强。

（3) 图4-28给出的是不同R./R;取值下K1值随φ的变化关系图

  R./R;这一参数间接反映了管道壁厚情况，数值越大说明管道的壁越厚。由图可以看到，5条曲线随角度的增大均向下递减，在开始段 0°~30°下降很快，之后趋于平缓，说明对不同的R./R;都有在自由表面的K1大于纹深处的K1.沿纵坐标观察的结果是，随着R./R;的增大，即随着管壁增厚，K1值呈增大趋势，且在裂纹自由面附近增加较多。这说明弯管的壁越厚，裂纹前缘附近应力奇异的程度越高，弯管就越不安全。

（4)图4-29给出的是不同M.取值下K,值随＠的变化关系图

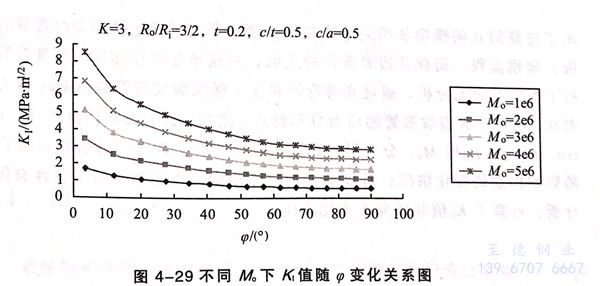
根据经验，弯管所受荷载越大，K1值应该越大。本图清晰地显示出这一规律。

（5)图4-30给出的是不同K取值下K1值随φ的变化关系图

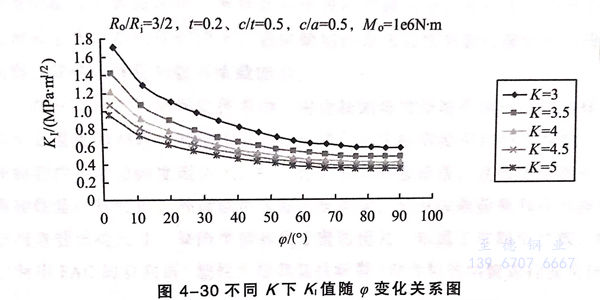
K 是弯曲半径与弯管外径的比值，K越大，曲率越小，弯管弯曲的程度越小，过渡更平缓。沿纵坐标观察曲线可以发现，随着弯管弯曲半径的减小，即弯管弯曲程度越高，K1值会越大。